Torna all'indice

Nel capitolo precedente sono stati analizzati i modelli teorici dello stato vetroso: sulla base di modelli strutturali si tenta di dare una spiegazione scientifica alla formazione di vetro da parte di certe sostanze. L’approccio cinetico alla cristallizzazione di liquidi sovraraffreddati descritto da Turnbull non cerca di scoprire le cause della formazione dello stato vetroso, limitandosi alla descrizione di come la velocità di raffreddamento, la densità nucleare o più in generale le proprietà dei materiali quali ad esempio la tensione superficiale liquido-cristallo o l’entropia di fusione possano influenzarne la formazione.

Due fattori principalmente influenzano la formazione dello stato vetroso da parte di un liquido sovraraffreddato:

1) la velocità di nucleazione ed accrescimento cristallino

2) la velocità di perdita di energia termica da parte del liquido in raffreddamento.

Uhlmann ha sviluppato le idee di Turnbull arrivando alla definizione di criteri guida nella formazione dello stato vetroso.

Se si stabilisce il rapporto tra la frazione in volume V_c del vetro che ha subito un processo di cristallizzazione e l’intero volume V sia pari ad X, nell’ipotesi che (tipicamente si considera = 10^-6 ) si può utilizzare la seguente equazione che è valida per piccoli valori di X e nel caso di materiali singolo componente o composti che fondono in modo congruente sempre che la frequenza di nucleazione e la velocità di crescita cristallina siano costanti:

dove I_v è la velocità di nucleazione per unità di volume ed u è la velocità di accrescimento (entrambi considerate costanti nel tempo e inversamente proporzionali alla viscosità).

Nella cristallizzazione ( transizione di fase a ® b ) il grado di conversione X_t al tempo t è dato dal rapporto dove V_t^b è il volume della fase b al tempo t e V^a è il volume della fase iniziale.

Il volume v_t di una particella è uguale a dove u è la velocità di accrescimento nelle tre direzioni dello spazio, t è il tempo necessario alla formazione del nucleo e g è il fattore di forma.

La velocità di nucleazione I_v è data dal numero di nuovi nuclei formati n* per unità di volume nell’unità di tempo: .

Se v_t è il volume di un nucleo formato al tempo t e V^a dn è il numero di nuclei che si formano al tempo t allora il volume totale della nuova fase b al tempo t sarà dato dalla espressione:

Se possiamo trascurare la diminuzione del volume iniziale V^a in seguito alla cristallizzazione allora il grado di conversione al tempo t è dato da:

la precedente espressione può essere scritta in forma differenziale:

assumendo i nuclei in formazione come sferici e che u ed I_v siano indipendenti dal tempo allora

Integrando l’espressione precedente si ricava l’equazione proposta da Uhlmann

***

In questo modo è possibile costruire una curva che metta in relazione, per dati valori di frazione cristallizzata X, la temperatura di sottoraffreddamento ed il tempo. Questa curva è anche detta curva T-T-T (time-temperature-trasformation) e con essa è possibile valutare le velocità critiche di raffreddamento per il passaggio liquido sottoraffreddato-vetro.(Fig1)

Fig.1 isolinee di uguale frazione in volume di cristalli in una fase vetrosa

come si vede dalla figura, stabilita una data frazione cristallina si può calcolare il tempo che occorre per la sua formazione, altrimenti si può ricavare la frazione di fase cristallina presente ad una certa temperatura di sottoraffreddamento dopo un tempo dato.

La curva T-T-T può essere anche calcolata sperimentalmente con tecniche in microscopia elettronica calcolando a temperature di sottoraffreddamento e tempi diversi il rapporto:

Il tempo t _n corrispondente al "naso" della curva è relativo al più breve tempo richiesto affinché si inizi a valutare quella data cristallizzazione. § 3.1

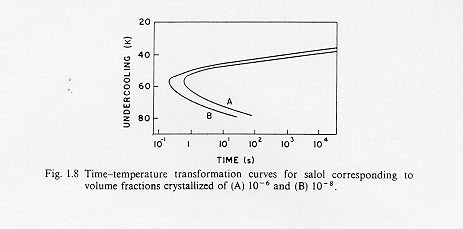
La curva T-T-T è il risultato della competizione tra la forza che induce la cristallizzazione e che aumenta al diminuire della temperatura e la mobilità atomica che diminuisce al diminuire della temperatura : questo effetto è rappresentato dalla presenza ad un certo tempo t di un punto di trasformazione (A), vicino al punto di fusione, dove la trasformazione é guidata dalla mobilità ionica ed un punto di trasformazione (B) dove la trasformazione é guidata dalla "driving force " della cristallizzazione, inoltre ,come vediamo per i punti c e c¹ di figura 1 , il tempo di trasformazione è relativamente lungo nelle vicinanze del punto di fusione ma anche a temperature molto più basse.

La minima velocità di raffreddamento necessaria per evitare la cristallizzazione è espressa dalla seguente espressione, la conoscenza delle curve T-T-T rappresenta quindi un valido aiuto nella determinazione dei cicli di formatura e di raffreddamento del vetro.

Fig 2

nella figura 2 sono descritte le principali trasformazioni di fase che avvengono nello stato vetroso,qui ci occuperemo della cristallizzazione lasciando la trattazione della separazione liquido-liquido ad un capitolo successivo.

Un vetro può cristallizzare in una fase con identica composizione chimica oppure con una composizione affatto diversa, lasciando in questo caso una fase vetrosa residua di composizione completamente diversa da quella di partenza.

La cristallizzazione può avvenire con due meccanismi principali:

1. la cristallizzazione di superficie :

essa avviene all’interfaccia tra l’atmosfera ed il fuso: la crescita cristallina è in questo caso generalmente orientata in modo radiale alla superficie di separazione.

2. la cristallizzazione di volume

essa ha inizio da siti di cristallizzazione nella massa del vetro fuso e può essere indotta da disomogeneità presenti come germi cristallini (cristallizzazione eterogenea) , nel caso che non siano presenti disomogeneità si parla invece di cristallizzazione omogenea.

3) teoria della nucleazione omogenea (Turnbull)

Sottoponendo un liquido ad un processo di raffreddamento la sua cristallizzazione dipende dalla crescita di cristalli a partire da un determinato numero di nuclei che possiedono una certa velocità di accrescimento.

La formazione di un vetro sarà allora legata ad una bassa velocità di accrescimento cristallino o ad una bassa velocità di formazione dei nuclei o ad una combinazione di entrambe i fattori.

La stabilità di una particella dipende da due contributi:

1) La differenza in energia libera tra la fase liquida e cristallina

2) L’energia interfacciale

Mentre al punto di fusione l’energia libera delle fasi liquida e cristallina è la stessa a temperature più basse il cristallo avrà energia libera più bassa: questo si traduce nel fatto che se ci sono nuclei di cristallizzazione il liquido tende naturalmente a cristallizzare.

Esiste cioè una "driving force" della cristallizzazione definibile dalla relazione fondamentale della termodinamica:

(1)

ma alla temperatura di fusione l’entalpia di fusione è circa uguale alla differenza tra l’entalpia dello stato liquido e quella dello stato solido, lo stesso dicasi per l’entropia di fusione:

(2)

d’altra parte poiché abbiamo detto che alla fusione la differenza di energia libera delle fasi liquida e cristallina è zero dalla (1) e (2) deriva:

alla temperatura di fusione T_f

.

quindi sempre dalla (1) la sarà

.

dove è il sovraraffreddamento: la dirving force per la cristallizzazione sarà tanto maggiore quanto maggiore è la temperatura di sottoraffreddamento.

In una trasformazione liquido-cristallo G_S é sempre minore della G_L e quindi la driving force sempre positiva, cioè perché vi sia cristallizzazione deve essere rispettata la condizione . Per la stessa ragione la variazione della energia libera durante la nucleazione sarà data da un termine negativo che tiene conto della trasformazione di fase e di un secondo termine positivo dovuto alla formazione di nuova interfaccia.

(3)

r = raggio del nucleo in formazione (ipotesi del nucleo sferico)

s = energia superficiale

Fig 3.

come si vede dalla figura 3 scomponendo i due termini per piccoli valori di r domina il termine quadratico e quindi sarà positivo (linea intera), con l’aumentare di r il termine cubico finisce per prendere il sopravvento e diminuisce a valori negativi.

La nucleazione omogenea è quindi un processo di attivazione con una barriera energetica (stato stazionario) da superare.

Derivando la nell’espressione (3) rispetto ad r ed eguagliando a zero si calcola il cosiddetto raggio critico r^*:

(4)

Questa espressione ci dice innanzitutto che maggiore è la driving force per il passaggio di stato minore è il raggio critico che si deve raggiungere perché la nucleazione avvenga spontaneamente.

Le particelle di raggio r < r^* sono chiamate embrioni e sono instabili poiché una loro riduzione in raggio, anche infinitesimale, è accompagnata dalla diminuzione di energia libera, esse sono quindi naturalmente destinate a ridisciogliersi nel fuso.

Particelle di raggio r > r^* sono chiamate nuclei e sono stabili poiché ogni loro aumento delle dimensioni, anche infinitesimale, è accompagnato dalla diminuzione dell’energia libera.

Si può calcolare il valore della barriera energetica del processo attivato semplicemente sostituendo l’espressione (4) nella (3):

(5)

se v è il volume di un atomo allora il volume di un "nucleo" che contiene n atomi sarà nv (ipotizzando il nucleo sferico):

(6)

sostituendo nella (6) il valore di r^* si ottiene il numero di atomi di quegli embrioni arrivati alle dimensioni critiche necessarie per diventare nuclei:

(7)

Poiché la formazione di un nucleo comporta una variazione positiva nell’energia libera si può calcolare la probabilità ( che sarà piccola) associata ad un tale evento.

La formazione di particelle di raggio critico sarà guidata da locali fluttuazioni di densità nucleare intorno ad uno stato stazionario definito dalla barriera energetica di figura 3; supponendo dunque una situazione di equilibrio termodinamico tra i clusters cristallini di raggio r^* e gli atomi del liquido circostante si può definire una costante di equilibrio K:

.

dove N_r è il numero di clusters di raggio r ed N è il numero di atomi per unità di volume della fase iniziale.

Assumendo che il sistema sia in equilibrio e che N_r << N la costante K è correlata a D G^* dalla relazione termodinamica di Boltzmann

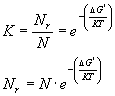(8)

in questa situazione l’addizione di un singolo atomo permette all’embrione di diventare nucleo. La velocità di formazione dei nuclei sarà data dal prodotto del numero di nuclei con raggio critico r* nell’unità di volume per la velocità con la quale atomi del liquido circostante si attaccano all’embrione.

Il numero di eventi per secondo nei quali un atomo riesce a superare l’interfaccia liquido-embrione è in relazione con la frequenza vibrazionale dell’atomo dove è la costante di Plank mentre la probabilità P che un evento abbia successo sarà data dall’espressione generale derivata dalla statistica di Bolzmann:

.

solo gli atomi adiacenti all’interfaccia sono nella situazione favorevole per potersi attaccare all’embrione, se il loro numero è N_s allora il numero di atomi N_a che attraverserà l’interfaccia per unità di tempo sarà dato da:

(9)

poiché la velocità di nucleazione è data dal prodotto del numero di cluster presenti in equilibrio nel liquido per la velocità di passaggio degli atomi attraverso l’interfaccia embrione-liquido degli atomi del liquido per la (8) ed (9) si ha:

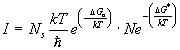(10)

Il secondo termine della (10) è in relazione alla probabilità che a temperatura T si abbia la formazione di nuclei con raggio superiore a quello critico: D G^* é chiamato barriera termodinamica alla nucleazione; il primo termine della (10) è invece in relazione alla diffusione atomica attraverso l’interfaccia durante la formazione del nucleo e D G_a é detto barriera cinetica alla nucleazione.

Sostituendo in (10) il valore di D G^* della (5) si trova che la velocità di nucleazione è molto sensibile a piccole variazioni di temperatura: calcolando il caso dell’H₂O vediamo che a -40°C la velocità di nucleazione aumenta di circa un fattore 9 per 1°C di abbassamento della temperatura.

Fig.4

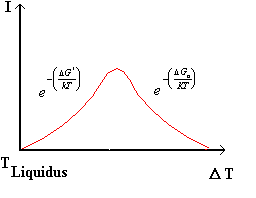
la figura 4 mostra la dipendenza della velocità di nucleazione con la temperatura di sottoraffreddamento D T; alla temperatura di liquidus il termine sarà pari a zero ed aumenterà mano a mano che D T aumenta (tratto ascendente), ad un certo valore di sovraraffreddamento prevarrà il termine cinetico e la velocità di nucleazione comincerà a decrescere dopo essere passata per un massimo.

Nella nucleazione eterogenea i nuclei si sviluppano alla superficie di un substrato che può essere costituito dalle pareti del contenitore, dall’interfaccia fuso-atmosfera o da una fase cristallina dispersa. La figura § 3.3 mostra un cluster formatosi sul substrato solido con un angolo di contatto pari a q .

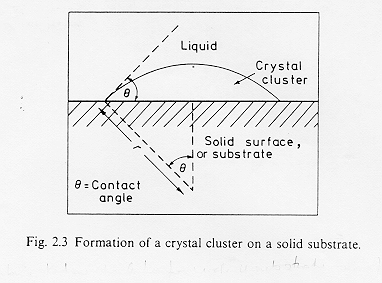
L’equazione della variazione dell’energia libera diventa:

(11)

dove V_c è il volume del cluster, V_m è il volume molare della fase cristallina, S_lc e S_cs sono le superfici delle interfacce liquido-cristallo e cristallo-substrato e le s sono le varie energie interfacciali. Assumendo che il cluster sia una calotta sferica di raggio r che le tre fasi (liquido, cristallo, e substrato) siano in equilibrio e che il substrato sia perfettamente piano si ha:

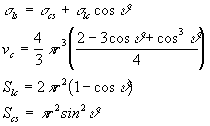(12)

sostituendo i valori in (12) nella (11) si ottiene, derivando rispetto ad r ed uguagliando a 0 il valore dell’espressione di r^*

(13)

vediamo che il valore di r^* è simile a quello ricavato dalla nucleazione omogenea (4) , sostituendo in (11) la (13) troviamo:

(14)

Il valore della barriera energetica è in funzione dell’angolo q di contatto ed è minore di quello della nucleazione omogenea dal momento che f(f ) £ 0 per 0 £ q £ p .

Infatti la relazione tra la barriera energetica nella cristallizzazione eterogenea e quella della cristallizzazione omogenea è data dalla relazione:

E’ facile dimostrare che per q = 180° , per q = 0 e che per sarà

Quindi la presenza del substrato causa un abbassamento nella barriera termodinamica alla nucleazione; un basso valore di si ottiene per bassi valori dell’angolo q cioè in pratica quando tra fase cristallina e substrato c’è una elevata superficie di contatto.

Introducendo un substrato opportuno in un liquido possiamo quindi ridurre la barriera alla nucleazione favorendo la nucleazione. Nel capitolo precedente abbiamo visto che la nucleazione eterogenea è favorita da un piccolo angolo di contatto tra cluster cristallino e substrato tuttavia se introduciamo nel liquido sottoraffreddato un seme cristallino che abbia, nei piani cristallini con indice basso, arrangiamenti atomici simili a quelli di analoghi piani cristallini della fase che viene nucleata, si assiste allora ad una cristallizzazione preferenziale orientata su di una faccia del seme cristallino.

Un esempio è dato dal disilicato di litio (cristallo ortorombico) che cristallizza sulla superficie di platino: il piano [111] del platino si sovrappone entro un errore del 6% con il piano [200] del disilicato di litio.

L’importanza della nucleazione eterogenea si apprezza nel campo dei vetro-ceramici: si distinguono due principali classi di nucleanti:

1) quelle sostanze capaci di formare cristalli con bassa solubilità nel vetro (come quelle che hanno tendenza a subire una riduzione allo stato elementare: Pt, Au, Ag, Cu)

2) Le sostanze come TiO₂, ZrO₂, P₂O₅ che, solubili nei vetri silicatici, aggiunte in quantità elevate (1-20%) in peso precipitano come composti cristallini quali Titanati o zirconati).

Essa dipende dal numero per unità di tempo di atomi del fuso che arrivano alla superficie del nucleo e vi rimangono accrescendo così il cristallo.

Se consideriamo l’interfaccia liquido-cristallo piana, trascurando cioè l’incremento dell’energia libera superficiale dovuta alla curvatura del nucleo nei primi stadi di crescita, si può dire che tutti gli atomi che arrivano all’interfaccia liquido-cristallo sono capaci di legarsi al cristallo per incrementare la fase solida in modo uniforme e in tutti i punti della superficie del cristallo.

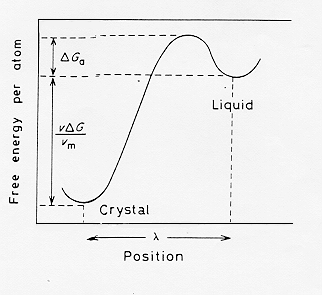
Gli atomi per poter superare l’interfaccia tra liquido e solido devono superare una energia di attivazione D G_a mentre il numero i di atomi che riescono a superare questa barriera per unità di tempo è dato dalla espressione:

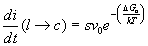(15)

s = numero di atomi del liquido che circondano il cristallo

v₀ = frequenza di vibrazione termica

il termine esponenziale rappresenta la probabilità di trovare un atomo della fase liquida con sufficiente energia termica da potersi attaccare al cristallo.

Una volta che un atomo ha oltrepassato l’interfaccia la sua energia è ridotta rispetto a quella di atomo nella fase liquida di un fattore dove v è il volume occupato da un atomo e v_m è il volume molare della fase cristallina.

Quindi per un atomo che passa dalla fase solida a quella liquida l’energia di attivazione richiesta è più alta che non per il passaggio inverso e quindi il numero di questi, passaggi per unità di tempo è dato da:

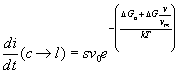(16) .

quindi il passaggio netto di atomi dallo stato liquido a quello cristallino è dato da

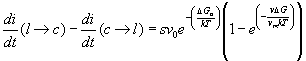
se si trasferiscono sulla fase solida s atomi allora il cristallo si accresce di l (dove l è approssimativamente la distanza interatomica la velocità di accrescimento u sarà allora:

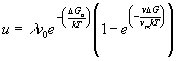(17)

poiché dove R è la costante dei gas, la (17) si semplifica nella Equazione Hilling-Turnbull:

(18)

la figura 3.5 mostra l’andamento della velocità di accrescimento cristallino in relazione alla temperatura di sottoraffreddamento

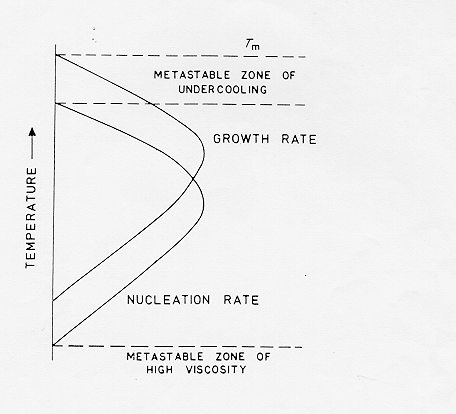
questa equazione (18) predice l’esistenza di un massimo nella velocità di accrescimento, infatti il secondo termine (termodinamico) della (18) aumenta all’aumentare del sovraraffreddamento mentre il primo termine (cinetico) diminuisce. Per un piccolo sottoraffreddamento il secondo termine è e quindi u é proporzionale a D G e quindi a D T. Per grandi sovraraffreddamenti l’esponente al secondo termine diventa molto piccolo, rimane così solo il primo termine ed u diventa proporzionale ad 1/T. Si noti anche come la massima velocità di crescita si abbia a D T più piccoli che nel caso della velocità di nucleazione: quindi in raffreddamento avremo pochi nuclei che si accrescono rapidamente (macrocristalli) mentre in ricottura molti nuclei che si accrescono più lentamente (microcristalli), questa è la situazione dei vetroceramici.

La figura 3.6 mostra le curve delle velocità di accrescimento cristallino e di nucleazione, in genere il massimo della velocità di crescita cristallina è a temperature di sottoraffreddamento minori rispetto al massimo della velocità di nucleazione

***

Nel caso in cui si consideri la diminuzione di volume della fase iniziale a durante la cristallizzazione il prodotto v_t dn* deve essere moltiplicato per la fase residua (1-X_t ) al tempo t:

riarrangiando l’equazione precedente

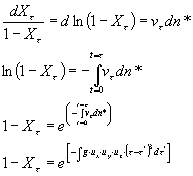
a seconda di come avviene la nucleazione e l’accrescimento cristallino l’integrazione di questa equazione detta KJMA (Kolmogorov-Johnson-Mehl-Avrami) può evolvere in diverse forme finali: ad esempio un accrescimento isotropico (u_x = u_y = u_z) di una particella sferica con velocità di nucleazione I_v costante nel tempo darà

torna da capo

torna all'indice